Optimization Toolbox 6.0
14Pages

Optimization Toolbox 6.0 table.main {} tr.row {} td.cell {} div.block {} div.paragraph {} .font0 { font:5.00pt "Arial", sans-serif; } .font1 { font:7.00pt "Arial", sans-serif; } .font2 { font:9.00pt "Arial", sans-serif; } .font3 { font:10.00pt "Arial", sans-serif; } .font4 { font:20.00pt "Arial", sans-serif; } .font5 { font:7.00pt "Courier New", monospace; } .font6 { font:8.00pt "Times New Roman", serif; } .font7 { font:14.00pt "Times New Roman", serif; } Optimization Toolbox 6.0 Solve standard and large-scale optimization problems Optimization Toolbox provides widely used algorithms for standard and large-scale optimization. These algorithms solve constrained and unconstrained continuous and discrete problems. The toolbox includes functions for linear programming, quadratic programming, binary integer programming, nonlinear optimization, nonlinear least squares, systems of nonlinear equations, and multiobjective optimization. You can use them to find optimal solutions, perform tradeoff analyses, balance multiple design alternatives, and incorporate optimization methods into algorithms and models. Key Features ■ Interactive tools for defining and solving optimization problems and monitoring solution progress ■ Solvers for nonlinear and multiobjective optimization ■ Solvers for nonlinear least-squares, data fitting, and nonlinear equations ■ Methods for solving quadratic and linear programming problems ■ Methods for solving binary integer programming problems ■ Parallel computing support in selected constrained nonlinear solvers Finding a local minimum of the peaks function using a gradient-based optimization solver from Optimization Toolbox. MathWorks- Accelerating the pace of engineering and science

Optimization Toolbox 6.0 table.main {} tr.row {} td.cell {} div.block {} div.paragraph {} .font0 { font:5.00pt "Arial", sans-serif; } .font1 { font:7.00pt "Arial", sans-serif; } .font2 { font:9.00pt "Arial", sans-serif; } .font3 { font:8.00pt "Times New Roman", serif; } .font4 { font:14.00pt "Times New Roman", serif; } - - x 1 A blurred image recovered using the large-scale linear least-squares algorithm. Defining, Solving, and Assessing Optimization Problems Optimization Toolbox includes the most widely used methods for performing minimization and maximization. The toolbox implements both...

Optimization Toolbox 6.0 table.main {} tr.row {} td.cell {} div.block {} div.paragraph {} .font0 { font:5.00pt "Arial", sans-serif; } .font1 { font:7.00pt "Arial", sans-serif; } .font2 { font:8.00pt "Arial", sans-serif; } .font3 { font:9.00pt "Arial", sans-serif; } .font4 { font:8.00pt "Times New Roman", serif; } .font5 { font:15.00pt "Times New Roman", serif; } An optimization routine running at the command line (left) that calls MATLAB files defining the objective function (top right) and constraint equations (bottom right). The Optimization Tool simplifies common optimization tasks. It...

Optimization Toolbox 6.0 table.main {} tr.row {} td.cell {} div.block {} div.paragraph {} .font0 { font:5.00pt "Arial", sans-serif; } .font1 { font:7.00pt "Arial", sans-serif; } .font2 { font:8.00pt "Arial", sans-serif; } .font3 { font:8.00pt "Times New Roman", serif; } .font4 { font:15.00pt "Times New Roman", serif; } V C:\MATl.Aft\wark\VropHm, m Q( Unconstrained nonlinear programming used to search an engine performance map for peak efficiency. Constrained Nonlinear Optimization Constrained nonlinear optimization problems are composed of nonlinear objective functions and may be subject to...

Optimization Toolbox 6.0 table.main {} tr.row {} td.cell {} div.block {} div.paragraph {} .font0 { font:5.00pt "Arial", sans-serif; } .font1 { font:7.00pt "Arial", sans-serif; } .font2 { font:9.00pt "Arial", sans-serif; } .font3 { font:8.00pt "Times New Roman", serif; } .font4 { font:15.00pt "Times New Roman", serif; } ■ Finite diffrence of gradients, without requiring knowledge of sparsity structure For the trust-region reflective algorithm, you can use: ■ Finite difference of gradients, Hessian with known sparsity structure ■ Actual Hessian (sparse or dense) ■ Hessian-multiply function...

Optimization Toolbox 6.0 table.main {} tr.row {} td.cell {} div.block {} div.paragraph {} .font0 { font:5.00pt "Arial", sans-serif; } .font1 { font:7.00pt "Arial", sans-serif; } .font2 { font:8.00pt "Arial", sans-serif; } .font3 { font:9.00pt "Arial", sans-serif; } .font4 { font:8.00pt "Times New Roman", serif; } .font5 { font:15.00pt "Times New Roman", serif; } ■ The minimax problem involves minimizing the worst-case value of a set of multivariate functions, possibly subject to linear and nonlinear constraints. Optimization Toolbox transforms both types of multiobjective problems into...

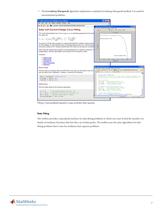
Optimization Toolbox 6.0 table.main {} tr.row {} td.cell {} div.block {} div.paragraph {} .font0 { font:5.00pt "Arial", sans-serif; } .font1 { font:7.00pt "Arial", sans-serif; } .font2 { font:8.00pt "Arial", sans-serif; } .font3 { font:8.00pt "Times New Roman", serif; } .font4 { font:15.00pt "Times New Roman", serif; } The Levenberg-Marquardt algorithm implements a standard Levenberg-Marquardt method. It is used for unconstrained problems. Fitting a transcendental quation using nonlinear least squares. Data Fitting The toolbox provides a specialized interface for data fitting problems in...

Optimization Toolbox 6.0 table.main {} tr.row {} td.cell {} div.block {} div.paragraph {} .font0 { font:5.00pt "Arial", sans-serif; } .font1 { font:7.00pt "Arial", sans-serif; } .font2 { font:8.00pt "Arial", sans-serif; } .font3 { font:8.00pt "Times New Roman", serif; } .font4 { font:15.00pt "Times New Roman", serif; } Fitting a nonlinear exponential quation using least-squares curve fitting. Nonlinear Equation Solving Optimization Toolbox implements a dogleg trust-region algorithm for solving a system of nonlinear quations where there are as many equations as unknowns. The toolbox can also...